1. Определение кольца. Делимость. Главные идеалы. Общее определение идеала. Кольца главных идеалов, наибольший общий делитель, разложение на простые множители. Евклидовы кольца. Факторкольцо по идеалу.
2. Кольцо целых чисел, евклидовость кольца Z. Алгоритм Евклида. Сравнения. Полная и приведенная системы вычетов. Обратимые элементы в кольце 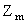. Функция Эйлера, теоремы Эйлера и Ферма. Линейные сравнения с одним неизвестным.
3. Кольцо многочленов одного неизвестного над полем. Алгебраическая и функциональная точки зрения. Корни многочленов. Теорема Безу, схема Горнера, разложение многочлена по степеням линейного двучлена.
4. Евклидовость кольца многочленов. Алгоритм Евклида. Неприводимые многочлены, разложение многочлена на неприводимые множители.
5. Кратные неприводимые множители, их отделение.
6. Кольца С[x] и R[x].
7. Кольцо Q[x]. Редукция к кольцу Z[x]. Теорема Гаусса. Критерий Эйзенштейна. Рациональные корни целочисленных многочленов.
8. Кольцо многочленов от некоторых неизвестных над полем. Симметрические многочлены.
9. Границы действительных корней многочленов. в кольце R[x]. Теорема Штурма.
10. Поле алгебраических чисел. Строение простого алгебраического расширения.

---

Университет | Отделение прикладной математики | Рабочие программы