Количество часов:
Лекции - 34
Практические занятия - 34
Консультации - 7
Экзамен
Составитель: доцент Васильева Т. В.

№ n/n	Содержание занятий	Лекции	Практ. занятия	Самост. работа	Форма контроля
I. 1.	Теория кривых Векторная функция скалярного аргумента. Понятие кривой. Способы задания линий. Примеры. Простая линия.	2
2.	Гладкие и регулярные кривые. Касательная.	2	2
3.	Длина дуги кривой. Естественная параметризация.	1	2
4.	Кривизна гладкой кривой.	1
5.	Сопровождающий трехгранник кривой (репер Френе). Соприкасающаяся плоскость.	2	2
6.	Формулы Френе. Понятие о натуральных уравнениях кривой.	2	2+2 к/р		Контр. работа
II. 1.	Теория поверхностей. Понятие поверхности. Способы задания элементарных поверхностей. Простая поверхность. Координатные линии. Задание линий на поверхности.	2	2
2.	Гладкие и регулярные поверхности. Примеры. Достаточное условие гладкости. Касательная плоскость и нормаль к поверхности.	2	2
3.	Первая квадратичная форма поверхности и ее приложения.	2	2
4.	Вторая квадратичная форма поверхности. Кривизна кривой на поверхности.	2	2
5.	Индикатриса Дюпена. Классификация точек поверхности.	2
6.	Главные направления и главные кривизны поверхности.	2			Контр.
7.	Гауссова и средняя кривизна. Поверхности постоянной гауссовой кривизны.	2	2+2к/р		работа и индив. задание.
III. 1.	Внутренняя геометрия поверхностей. Основные уравнения теории поверхностей.	1
2.	Изометричные поверхности. Понятие о внутренней геометрии поверхностей	1
3.	Геодезическая кривизна кривой на поверхности. Геодезические линии.	1
4.	Теорема Гаусса-Бонне и ее следствия.	1
IV. 1.	Дифференцируемые многообразия. Понятие карты, атласа, топологического многообразия. Примеры.	1
2.	Гладкие многообразия: определение и примеры.	1
3.	Гладкие функции на многообразии: определение, примеры.	2
4.	Касательный вектор( Связь касательного вектора и производной по направлению в 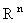). Касательный вектор в точке на многообразии. Касательное пространство и его размерность.	2
5.	Гладкие отображения. Диффеоморфизмы. Примеры.	1
6.	Дифференциал и ранг гладкого отображения.	1
7.	Понятие тензора в 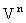. Основные операции над тензорами.	1
8.	Векторные и тензорные поля на многообразии.	1
9.	Кососимметричные тензоры. Альтернирование. Внешнее умножение кососиммтричных тензоров.	2
10.	Полилинейные формы. Внешнее умножение внешних форм.	2
11.	Дифференциальные формы в 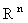. Внешний диффренциал внешней дифференциальной к-формы.	2
12.	Дифференциальные формы на многообразии.	1
13.	Интегрирование по многообразию. Формула Стокса.	1

1. Атанасян Л. С., Базылев В. Т. Геометрия. 4. 2. — М., 1987.
2. Атанасян Л. С. и др. Сборник задач по геометрии. 4. 2. — М., 1975.
3. Базылев В. Т. и др. Сборник задач по геометрии. — М., 1980.
4. Васильева М. В. Учебное пособие по дифференциальной геометрии. — М.: МГПИ, 1978.
5. Майоров В. М. и др. Задачи по объединенному курсу геометрии. — Ярославль, 1988.
6. Позняк Э. Г., Шикин Е. В. Дифференциальная геометрия: Первое знакомство. — М.: Издательство МГУ, 1990.
7. Рашевский П. К. Курс дифференциальной геометрии. — М., 1936.
8. Розендори Э. Р. Задачи по дифференциальной геометрии. — М., 1971.
9. Погорелов А. В. Дифференциальная геометрия. — М., 1974.
10. Сборник задач по дифференциальной геометрии. /Под ред. А. С. Феденко. — М., 1979.

Вопросы к экзамену по геометрии

для III курса

отделения прикладной математики:

1. Определение топологического пространства. Примеры. Открытые и замкнутые множества. Свойства замкнутых множеств.
2. Внутренние, внешние, граничные точки. Замыкание. Критерий открытости и замкнутости множества.
3. База топологии. Примеры. Критерий базы.
4. Связность. Теоремы о связных множествах.
5. Аксиомы отделимости.
6. Компактные топологические пространства. Компактные подмножества топологических пространств.
7. Непрерывные отображения топологических пространств. Критерий непрерывности. Свойства непрерывных отображений.
8. Гомеоморфизмы. Свойства гомеоморфизмов. Отношение топологической эквивалентности.
9. Линейная связность. Соответствие между связностью и линейной связностью.
10. Топология, индуцированная метрикой.
11. Карта. Атлас. Понятие многообразия. Примеры. Многообразие с краем.
12. Клеточное разложение многообразия. Эйлерова характеристика. Ориентируемые и неориентируемые многообразия.
13. Понятие линии. Способы задания линии. Примеры. Простая линия.
14. Гладкие и регулярные кривые. Гладкость и регулярность при различных способах задания.
15. Длина гладкой кривой. Естественная параметризация. Примеры.
16. Кривизна регулярной кривой.
17. Сопровождающий трехгранник кривой /репер Френе/. Геометрические свойства соприкасающейся плоскости.
18. Кручение регулярной кривой.
19. Формулы Френе. Понятие о натуральных уравнениях.
20. Понятие поверхности. Способы задания поверхностей. Примеры.
21. Гладкие и регулярные поверхности. Достаточный признак гладкости поверхности в точке. Примеры.
22. Криволинейные координаты. Координатные линии. Задание линий на поверхности. Касательная плоскость и нормаль к поверхности.
23. Первая квадратичная форма поверхности и ее приложения.
24. Вторая квадратичная форма. Примеры.
25. Нормальная кривизна кривой на поверхности.
26. Индикатриса Дюпена. Классификация точек поверхности.
27. Главные направления и главные кривизны. Уравнения главных направлений и главных кривизн.
28. Гауссова /полная/ и средняя кривизны поверхности. Поверхности постоянной полной кривизны.
29. Изометричные поверхности.
30. Геодезическая кривизна. Геодезические линию. Теорема Гаусса-Бонне и ее следствие.

---

Университет | Отделение прикладной математики | Рабочие программы