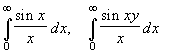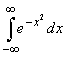1. Числовые ряды. Основные понятия
2. Положительные ряды, признаки сравнения, Даламбера, Коши
3. Знакопеременные ряды, признак Лейбница, перестановки рядов
4. Признаки Абеля и Дирихле
5. Сложение и умножение абсолютно и условно сходящихся рядов
6. Бесконечные произведения
7. Функциональные последовательности и ряды
8. Условия равномерной сходимости: критерий Коши, признак Вейерштрасса, признак Дини
9. Признаки Абеля и Дирихле равномерной сходимости
10. Функциональные свойства равномерно сходящихся функциональных последовательностей и рядов (переход к пределу, непрерывность, интегрируемость, дифференцируемость)
11. Равностепенная непрерывность, теорема Арцела, сходимость и компактность в
12. Степенные ряды, радиус и интервал сходимости, равномерная сходимость
13. Разложение функции в степенной ряд
14. Разложение элементарных функций в ряд Тейлора
15. Элементарные функции в комплексной области
16. Теорема Вейерштрасса об аппроксимации
17. Евклидовы пространства, ортонормированные системы
18. Понятие и примеры рядов Фурье, неравенство Бесселя, равенство Парсеваля
19. Преобразование тригонометрических сумм, теорема Фейера, ее следствия: замкнутость тригонометрической системы, теорема Вейерштрасса.
20. Лемма Римана, поточечная сходимость тригонометрических рядов Фурье
21. Равномерная сходимость тригонометрических рядов Фурье
22. Разложение в тригонометрический ряд, разложение синуса в бесконечное произведение
23. Понятие гильбертова пространства
24. Собственные интегралы с параметром, непрерывность, дифференцируемость, интегрируемость
25. Интегралы с пределами, зависящими от параметра
26. Несобственные интегралы с параметром (равномерная сходимость, критерий Коши, признак Вейерштрасса, признак Дирихле, примеры , )
27. Непрерывность, дифференцируемость несобственных интегралов с параметром, примеры
28. Интегрируемость несобственных интегралов с параметром, пример
29. Функции Эйлера
30. Формула Стирлинга
31. Интеграл Фурье и преобразование Фурье

Литература:

1. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ, МГУ, 1987. т.2.
2. Ильин В.А., Позняк Э.Г. Основы математического анализа, М., Наука, 1973. т.2.
3. Зорич В.А. Математический анализ, М., Наука, 1988, т.2.
4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М., Наука, 1969, т.2.

---

Университет | Отделение прикладной математики | Рабочие программы